2025年全国二卷数学高考真题带答案带解析带分值文字版
(网络收集)
2025年全国二卷数学高考真题带答案带解析带分值文字版
一、单选题:本题共8小题,每小题5分,共40分,每小题只有一个选项符合要求
1.样本数据2,8,14,16,20的平均数为
A.8
B.9
C.12
D.18
【答案】C
【解析】本题考查了样本平均数,考查运算能力![]()
故答案为C
【分值】5分
2.已知![]() ,则
,则![]()
A.![]()
B.![]()
C.-1
D.1
【答案】A
【解析】本题考查了复数的运算![]() ,
,![]()
【分值】5分
3.已知集合![]() ,
,![]() ,则
,则![]()
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】本题考查了集合的运算、交集、解方程.
由 B:![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
【分值】5分
4.不等式![]() 的解集是
的解集是
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】本题考查了解分式不等式![]() 移项:
移项:![]()
通分![]()
等价转化为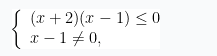
解得:![]()
【分值】5分
5.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]()
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】本题考查了余弦定理的应用.
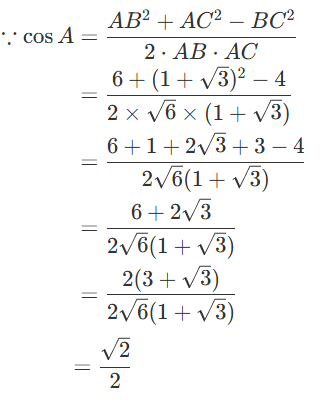
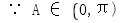 ,
,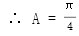
故选 .
.
【分值】5分
6.设抛物线C:![]() 的焦点为
的焦点为![]() ,点A在C上,过
,点A在C上,过![]() 作
作![]() 的准线的垂线,垂足为
的准线的垂线,垂足为![]() .若直线BF的方程为
.若直线BF的方程为![]() ,则
,则![]()
A.3
B.4
C.5
D.6
【答案】C
【解析】本题考查了抛物线的定义,考查了直线与抛物线的位置关系.
如图:
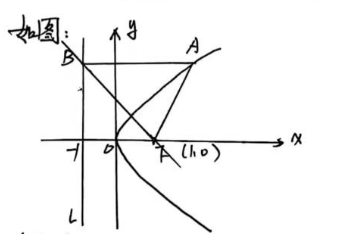
 直线
直线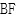 :
: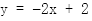 ,令
,令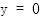 ,
,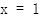
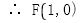 ,
,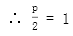 ,
,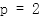
 抛物线方程为
抛物线方程为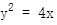
 准线方程为
准线方程为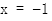
设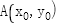 ,
,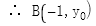
令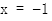 ,
,
则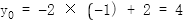
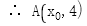 代入
代入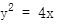 中,得
中,得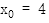
![]()
故选C.
【分值】5分
7.记![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() ,则
,则![]()
A.-20
B.-15
C.-10
D.-5
【答案】B
【解析】本题考查了等差数列的求和公式![]() ,
,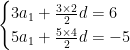
即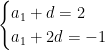
解得![]() ,
,![]()
![]()
故选B
【分值】5分
8.已知![]() ,
,![]() ,则
,则![]()
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】

![]()
![]()
故选D
【分值】5分
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.生部选对的得6分,部分选对的得部分分,有选错的得0分.
9.记![]() 为等比数列
为等比数列![]() 的前
的前![]() 项和,
项和,![]() 为
为![]() 的公比,
的公比,![]() 若
若![]() ,则
,则
A.![]()
B.![]()
C.![]()
D.![]()
【答案】AD
【解析】本题考查了等比数列的通项公式、等比数列的求和公式![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
整理得![]() ,解得
,解得![]() ,
,![]() (舍)
(舍)
故A正确![]() ,故B错误
,故B错误![]()
![]() ,故C错误
,故C错误![]()
![]()
![]()
故D正确
【分值】6分
10.已知![]() 是定义在
是定义在![]() 上的奇函数,且当x>0时,
上的奇函数,且当x>0时,![]() ,则
,则
A.![]()
B.当x<0时,![]()
C.![]() ,当且仅当
,当且仅当![]()
D.![]() 是
是![]() 的极大值点
的极大值点
【答案】ABD
【解析】本题考查了函数的奇偶性、对称性,导数研究函数的单调性、极值
∵![]() 在
在![]() 上为奇函数,
上为奇函数,![]() 时,
时,
![]()
设![]()
![]()
![]() ,
,![]()
当![]() 时,
时,![]()
故B正确
由奇函数的性质,![]() ,
,![]() ,故A正确
,故A正确
因为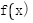 是奇函数,图像关于(0,0)对称,不妨先研究
是奇函数,图像关于(0,0)对称,不妨先研究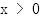 时
时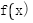 的性质,
的性质,
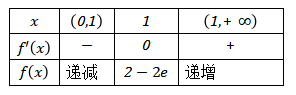
当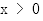 时,
时,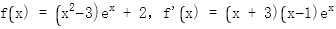
令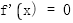 ,
,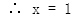
则 与
与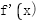 的情况如下表
的情况如下表
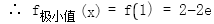
故由函数关于原点对称,其图像大致如下
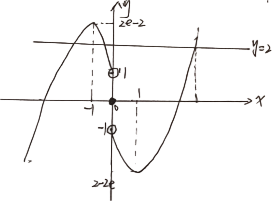
故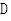 正确
正确
由图像可知,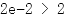 ,当
,当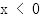 时,
时,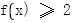 的解集不是空集,故
的解集不是空集,故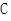 错误
错误
【分值】6分
11.双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,左、右顶点分别为
,左、右顶点分别为![]() .以
.以![]() 为直径的圆与曲线
为直径的圆与曲线![]() 的一条渐近线交于
的一条渐近线交于![]() 两点,且
两点,且![]() ,则
,则
A.![]()
B.![]()
C.![]() 的离心率为
的离心率为![]()
D.当![]() 时,四边形
时,四边形![]() 的面积为
的面积为![]()
【答案】ACD
【解析】本题考查了双曲线的性质,双曲线的渐近线,考查了直线与圆相交,以及求双曲线的离心率.
如图
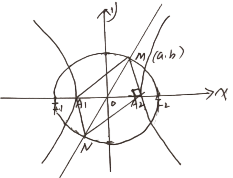
双曲线的渐近线为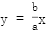
过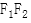 为直径的圆方程为
为直径的圆方程为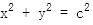
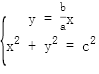
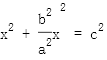
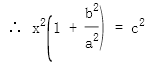
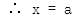
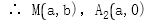
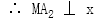 轴
轴
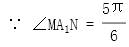
 ,A正确
,A正确
则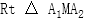 中,
中,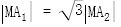 ,
,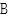 错误
错误
![]()
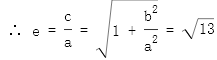
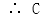 正确
正确
当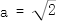 时,
时,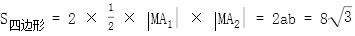 ,
,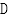 正确
正确
【分值】6分
三、填空题:本题共3小题,每小题5分,共15分
12.已知平面向量![]() ,
,![]() ,若
,若![]() ,则
,则![]() ____
____
【答案】![]()
【解析】本题考查了向量的坐标运算和向量垂直的条件及向量的模.
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
故答案为![]() .
.
【分值】5分
13.若![]() 是函数
是函数![]() 的极值点,则
的极值点,则![]() ____
____
【答案】-4
【解析】本题考查了利用导数研究函数的极值,由极值点求参数的值.
![]()
![]()
![]()
![]()
![]()
![]()
故答案为![]() .
.
【分值】5分
14.一个底面半径为![]() ,高为
,高为![]() 的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为____
的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为____![]() .
.
【答案】2.5
【解析】本题考查了立体几何中的球的切接问题.
如图:作出圆柱与球的轴截面
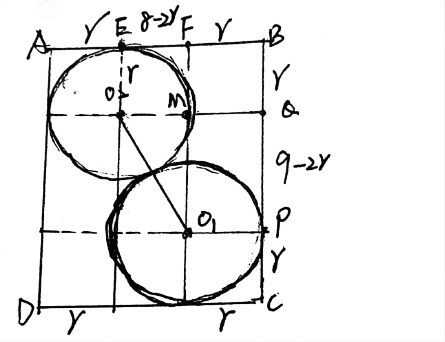
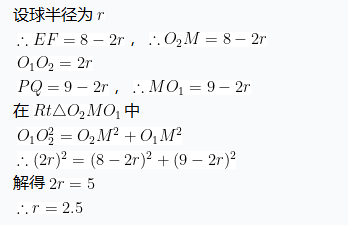
故答案为2.5
【分值】5分
![]() 四、解答题:本题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤
四、解答题:本题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤
15.已知函数
(1)求![]() .
.
![]() (2)设函数
(2)设函数![]() ,求
,求![]() 的值域和单调区间.
的值域和单调区间.
【答案】(1)
(2)g(x)的值域:![]() ,增区间:
,增区间:![]() 减区间:
减区间:![]()
【解析】本题考查了三角恒等变换、三角函数的值域和单调区间的求法

【分值】13分
16.已知椭圆![]() 的离心率为
的离心率为![]() ,长轴长为
,长轴长为![]() .
.
(1)求![]() 的方程.
的方程.
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 为坐标原点.若△OAB的面积为
为坐标原点.若△OAB的面积为![]() ,求
,求![]() .
.
【答案】(1)![]()
(2)![]()
【解析】本题考查了椭圆标准方程的求法,直线与椭圆的位置关系、弦长公式等知识.

【分值】15分
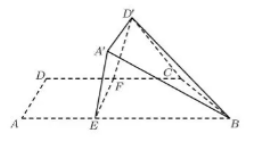
17.如图,四边形ABCD中,AB∥CD,∠DAB=90°,F为CD中点,E在AB上,EF∥AD,AB=3AD,CD=2AD.将四边形EFDA沿EF翻折至四边形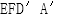 ,使得面
,使得面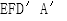 与面
与面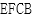 所成的二面角为
所成的二面角为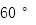 .
.
(1)证明: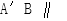 平面
平面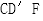 .
.
(2)求面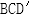 与面
与面 所成的二面角的正弦值.
所成的二面角的正弦值.
【答案】(1)见解析
(2)![]()
【解析】本题考查了线面平行的证明,及空间向量求二面角的知识.
(1) ![]()
![]()
![]() 面
面![]() ,
,![]() 面
面![]()
![]() 面
面![]()
![]()
![]()
![]() 面
面![]() ,
,![]() 面
面![]()
![]() 面
面![]()
又![]() ,EB,
,EB,![]() 面
面![]()
![]() 平面
平面![]() 面
面![]()
![]() 面
面![]()
![]() 面
面![]()
(2)由折叠关系知,![]() ,
,![]()
![]()
![]() ,
,![]()
不妨设![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() 为等边三角形
为等边三角形![]() ,
,![]() 面
面![]() ,取
,取![]() 中点
中点![]() ,连
,连![]()
可知![]() ,
,![]() ,
,![]() ,
,![]() 面
面![]()
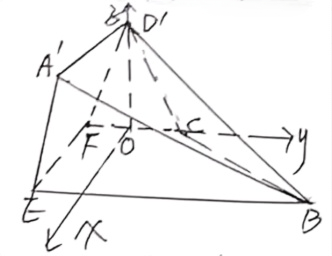
![]() 以
以![]() 为原点,与
为原点,与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系
![]()
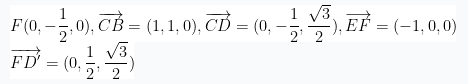
设平面![]() 的法向量为
的法向量为![]()
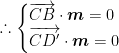 ,即
,即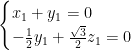 ,取
,取![]() ,则
,则![]() ,
,![]()
![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
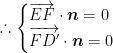 ,即
,即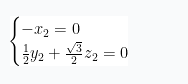 ,取
,取![]()
![]()
![]()
设平面![]() 与面
与面![]() (同前,应为
(同前,应为![]() )所成的二面角为
)所成的二面角为![]()
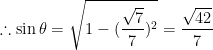
【分值】15分
18.已知函数![]() ,其中
,其中![]() .
.
(1)证明:![]() 在区间
在区间![]() 存在唯一的极值点和唯一的零点.
存在唯一的极值点和唯一的零点.
(2)设![]() ,
,![]() 分别为
分别为![]() 在区间
在区间![]() 的极值点和零点.
的极值点和零点.
①设函数![]() .证明:
.证明:![]() 在区间
在区间![]() 单调递减
单调递减
②比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
【答案】(1)见解析
(2)①见解析
②![]()
【解析】本题主要考查了函数的极值点和零点,利用导数证明函数的单调性,及比较大小.
(1) ![]()
![]()
令![]() 则
则![]() ,
,
令![]()
![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,
令![]()
![]() ,
,![]() 在
在![]() 单调递减
单调递减
![]() 在
在![]() 处取得极大值,
处取得极大值,
即![]() 在
在![]() 存在唯一极值点
存在唯一极值点
又![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,
![]() 在
在![]() 存在唯一零点.
存在唯一零点.
(2)①由(1)知![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
![]() ,即
,即![]() 在
在![]() 上单调递减
上单调递减

【分值】17分
19.甲、乙两人进行乒乓球练习,每个球胜者得![]() 分,负者得
分,负者得![]() 分.设每个球甲胜的概率为
分.设每个球甲胜的概率为![]() ,乙胜的概率为
,乙胜的概率为![]() ,
,![]() ,且各球胜负相互独立,对正整数
,且各球胜负相互独立,对正整数![]() ,记
,记![]() 为打完
为打完![]() 个球后甲比乙至少多得
个球后甲比乙至少多得![]() 分的概率,
分的概率,![]() 为打完
为打完![]() 个的球后乙比甲至少多得
个的球后乙比甲至少多得![]() 分的概率.
分的概率.
(1)求![]() ,
,![]() (用
(用![]() 表示).
表示).
(2)若![]() ,求
,求![]() .
.
(3)证明:对任意正整![]() ,
,![]() .
.
【答案】(1)![]()
(2)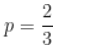
(3)见解析
【解析】(1) ![]()
![]()
![]()
![]()
![]()
(2) 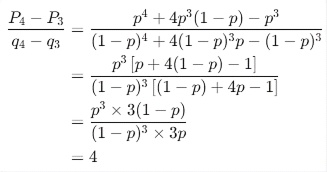
![]()
(3)记![]() 表示
表示![]() 球甲得
球甲得![]() 分的概率.
分的概率.![]()
![]()
故 ![]()
![]()
故要证:![]()
只需证:![]()
即只需证: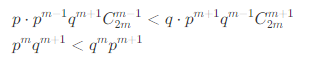
即![]() ,由条件
,由条件![]() ,故结论成立.
,故结论成立.
由![]()
![]()
现在,考虑不等式右边 ![]() .
.
只需证 ![]()
![]()
只需证:![]()
只需证 ![]()
只需证:![]()
因为![]() 且
且 ![]()
故上面不等式成立,证毕.
【分值】17分

